Lösertechnologie
Moderne CFD-Löser nutzen fortschrittliche numerische Methoden wie Finite-Volumen- und Finite-Elemente-Verfahren zur Lösung der Navier-Stokes-Gleichungen. Parallele Rechenverfahren auf CPU und GPU sowie Optimierungen verbessern die Effizienz. Zusätzliche Technologien umfassen adaptive Gitter, Turbulenzmodelle und multiphysikalische Kopplungen für realistische Simulationen.
Zu den eingesetzten Technologien gehören:
- explizite, sequentielle sowie implizite, gekoppelte Lösung der partiellen Differentialgleichungen auf Grundlage der Finiten-Volumen-Methode (FVM),
- algebraische Mehrgitterlöser für die effiziente Lösung der hochdimensionalen linearisierten Systeme,
- herausragende Paralleleffizienz, mit der die vorhandene Rechnerstruktur optimal ausgenutzt wird,
- umfangreiche physikalische Modelle zur Lösung Ihrer speziellen Fragestellung sowie
- weitreichende Möglichkeiten zur Anpassung an spezielle Anforderungen.
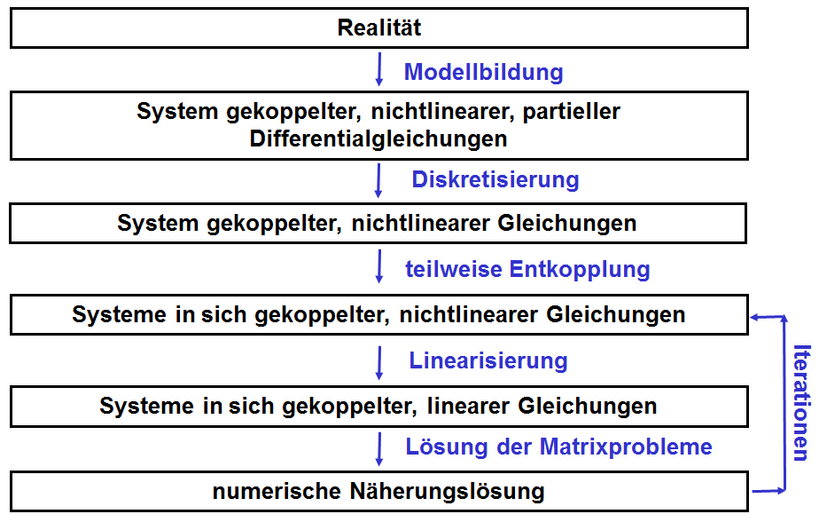
Mit Hilfe der Strömungssimulation soll die Realität, also die wirkliche Strömung in einem Bauteil, in einem Computer möglichst wirklichkeitsnah berechnet werden. Hierfür sind verschiedene Teilschritte erforderlich:
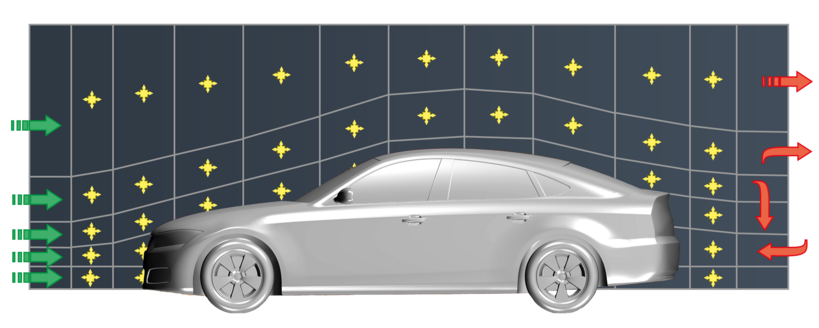
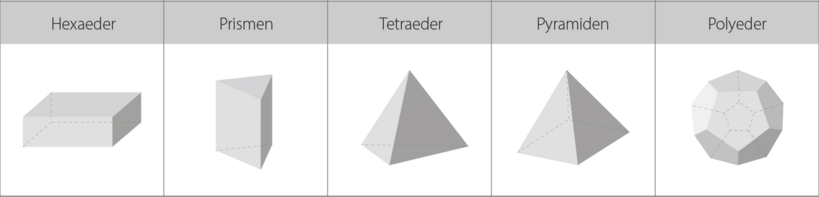
- Geometrie und Gitter: Der Nutzer legt fest, welcher Ausschnitt seiner Geometrie mit welcher Genauigkeit (Gitterauflösung) berechnet wird, welche Geometriedetails vernachlässigt werden können und wo die Fluide in seinen Geometrieausschnitt hinein- bzw. aus diesem herausströmen. Mehr dazu finden Sie im Bereich Modellerstellung.
- Modellbildung: Im Rahmen der Modellbildung entscheidet der Nutzer, mit welchem Materialmodellen seine Fluide abgebildet werden sollen und welche physikalischen Modelle berücksichtigt werden sollen. Außerdem legt er die entsprechenden Rand- und Anfangsbedingungen fest. Mehr dazu finden Sie im Bereich Physikalische Modelle.
- Diskretisierung: Ergebnis der Modellbildung ist ein System gekoppelter, nichtlinearer, partieller Differentialgleichungen mit entsprechenden Randbedingungen und weiteren algebraischen Gleichungen z.B. für die Materialgesetze. Diese werden auf der gegebenen Vernetzung räumlich und, bei transienten Rechnungen, mit der gegebenen Zeitschrittweite zeitlich diskretisiert.
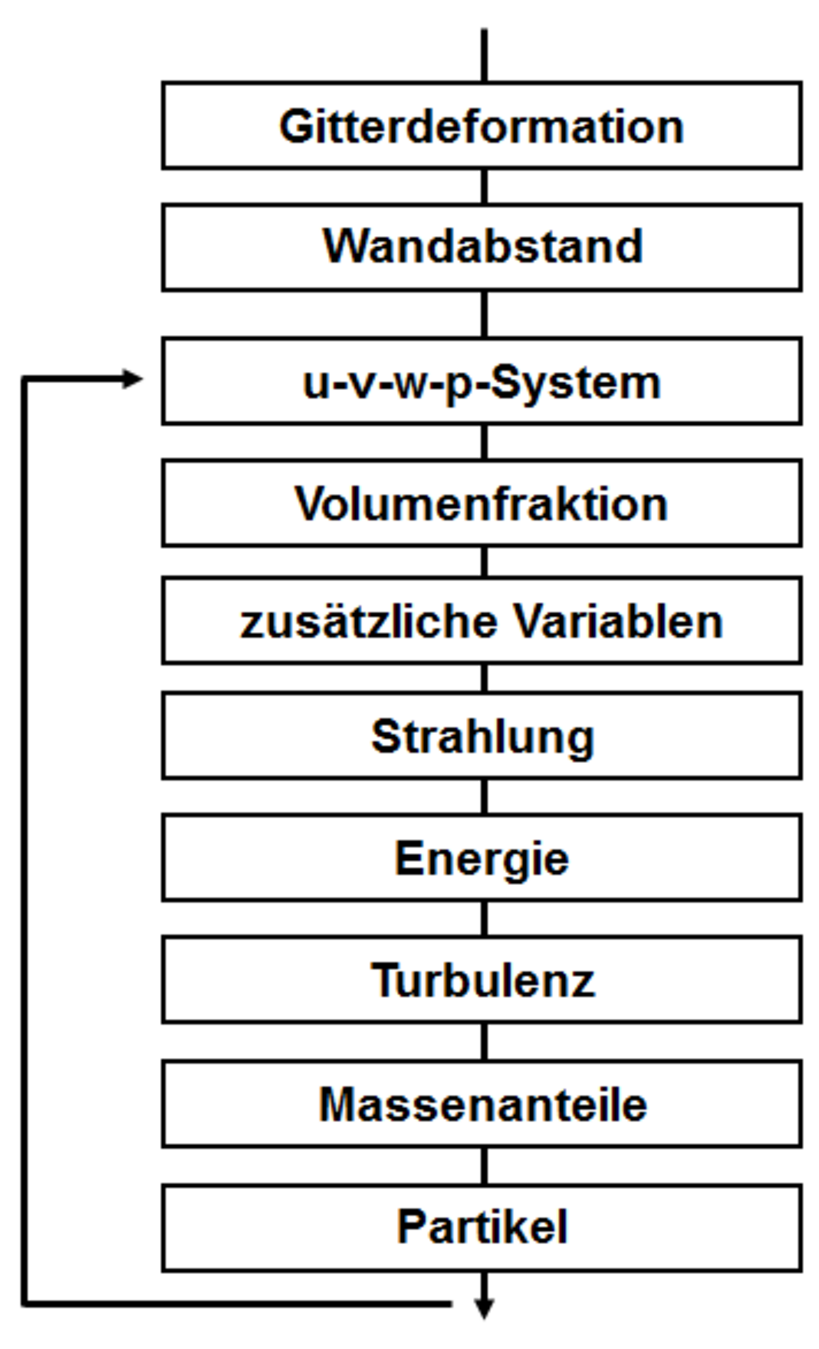
- Sequentielle oder gekoppelte Berechnung: Aus der Diskretisierung ergibt sich ein System gekoppelter, nichtlinearer, algebraischer Gleichungen sehr hoher Dimension (Produkt aus Knotenzahl und Anzahl partieller Differentialgleichungen). Diese können sequentiell (jede partielle Differentialgleichung einzeln) oder gekoppelt (alle zusammen) oder teilweise gekoppelt gelöst werden.
- Linearisierung: Das nichtlineare Gleichungssystem wird um die aktuelle Näherungslösung linearisiert, um es auf ein lineares Gleichungssystem zurückzuführen. Hierbei werden möglichst viele Terme implizit behandelt, um die Konvergenz zu verbessern, gleichzeitig muss aber beachtet werden, dass die Matrix nicht zu groß wird.
- Lösung der Matrixprobleme: Die sehr großen, aber dünnbesetzten linearen Matrixprobleme werden typischerweise nicht direkt gelöst, sondern über iterative Verfahren, oft Mehrgitter-Verfahren, wird eine Näherungslösung bestimmt.
- iterative Lösung: Durch die Entkopplung, die Linearisierung und die näherungsweise Lösung reicht die einmalige Durchführung nicht aus, um eine wirklichkeitsnahe Lösung zu erhalten, sondern diese Schritte werden mehrmalig, d.h. iterativ durchgeführt, bis eine vorgegebene Genauigkeit erreicht ist. Dann wird die Lösung ausgegeben bzw. der nächste Zeitschritt berechnet.
Untenstehend erfahren Sie genauer, wie diese einzelnen Schritte in CFD-Lösern implementiert wurden.
Zur numerischen Lösung der Navier-Stokes-Gleichungen müssen diese durch Diskretisierung in ein System algebraischer Gleichungen überführt werden. Maßgeblich für die Genauigkeit der erzielten Lösung ist die gewählte Form der räumlichen beziehungsweise zeitlichen Diskretisierung.
Die zeitliche Diskretisierung ist dafür verantwortlich, wie zeitliche Verläufe in transienten Berechnungen abgebildet werden. Unterschieden wird zwischen expliziten und impliziten Verfahren erster und zweiter Ordnung. Explizite Verfahren erster Ordnung (Euler-vorwärts) stellen die einfachste Form einer zeitlichen Diskretisierung dar und eignen sich aufgrund der begrenzten Zeitschrittweite (CFL-Kriterium) und des geringen Rechenaufwands vor allem für stark zeitabhängige Prozesse (Explosionen, Schallentstehung, -ausbreitung). Implizite Verfahren erster und zweiter Ordnung bieten eine höhere Stabilität und Genauigkeit auch bei großen Zeitschrittweiten und verkürzen dabei die Berechnung über längere Zeiträume beträchtlich.
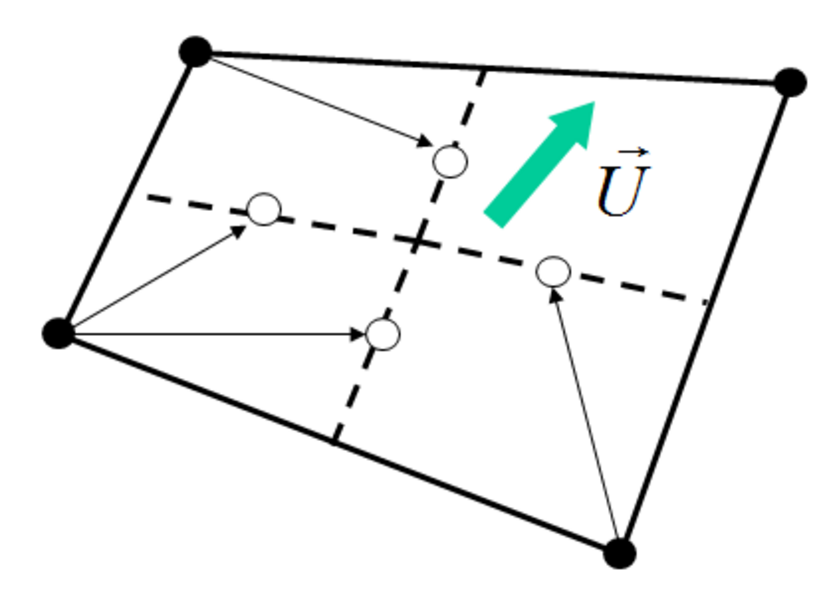
Die räumliche Diskretisierung ersetzt die Feldgrößen durch die Werte an den Knoten des Berechnungsgitters. CFD-Löser nutzen hierfür die Finite-Volumen-Methode, d.h. die partiellen Differentialgleichungen werden in ihrer konservativen Integralform durch Volumenbilanzen diskretisiert. Werte zwischen den Knoten oder Gradienten der Strömungsgrößen werden hierbei durch Interpolationsverfahren aus den Knotenwerten bestimmt. Verfahren erster Ordnung (Upwind) sind zwar sehr stabil und bilden Diskontinuitäten (Stöße) in der Strömung sehr gut ab, neigen jedoch dazu, Strömungen zu dissipativ vorherzusagen. Verfahren zweiter Ordnung sind weniger dissipativ, neigen jedoch zu Instabilitäten und Artefakten in der Lösung. CFD-Software enthält deshalb Diskretisierungsverfahren, welche lokal das Verfahren zwischen erster und zweiter Ordnung mittels eines Blend-Faktors wählen. Dabei wird die Ordnung des Diskretisierungsverfahrens möglichst hoch gewählt, um eine exakte Lösung zu garantieren.
Die Ordnung eines Verfahrens gibt an, wie schnell der Fehler des Verfahrens bei einer Verkleinerung der Diskretisierungsweite (Gitterabstand bzw. Zeitschrittweite) sinkt; der Fehler ist proportional der Weite potenziert mit der Ordnung.
Die Navier-Stokes-Gleichungen bilden ein System gekoppelter Differentialgleichungen (drei Impulsgleichungen in die Raumrichtungen, eine Kontinuitätsgleichung). Zur numerischen Lösung dieses Gleichungssystem bieten sich zwei Strategien an:
Sequentielle Berechnung: Bei diesem Verfahren werden alle vier Gleichungen nacheinander gelöst. Vorteile dieses Verfahrens sind der geringe numerische Aufwand für die Lösung einer einzelnen Gleichung. Da die Lösungen der einzelnen Gleichungen jedoch voneinander abhängen, muss die Lösung des Gesamtsystems iterativ bestimmt werden. Bei starken Wechselwirkungen der Gleichungen (große Druckgradienten, Eckenströmung) resultiert daraus eine hohe Anzahl an Iterationen bis zur exakten Lösung des Gleichungssystems.
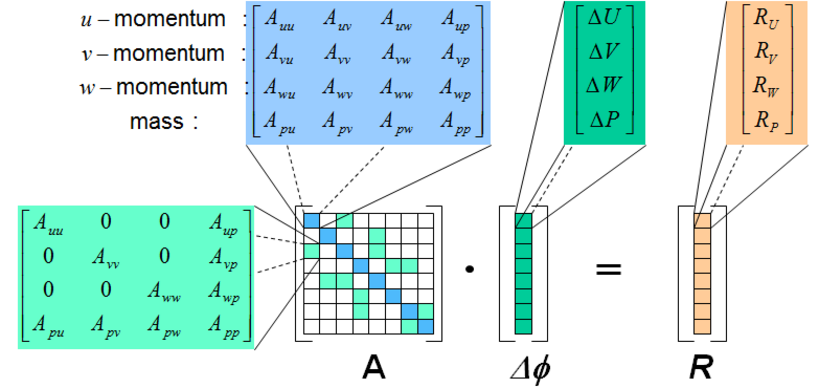
Gekoppelte Berechnung: Bei diesem Verfahren werden alle vier Gleichungen gemeinsam gelöst. Gegenüber dem sequentiellen Verfahren erlaubt dies die Verwendung eines bedeutend größeren Zeitschrittes. Damit verkürzt sich die Berechnungsdauer beträchtlich, obwohl im Vergleich zum sequentiellen Löser ein höherer Berechnungsaufwand pro Iteration erforderlich ist. In ganz besonderem Maße gilt dies bei Problemstellungen mit starken Wechselwirkungen zwischen den Gleichungen, wie zum Beispiel bei rotierenden Strömungsmaschinen, Mehrphasenströmungen oder Strömungen bei hohen Machzahlen mit starken Druckgradienten. Bei der Simulation von Mehrphasenströmungen fasst der gekoppelte Löser die hydrodynamischen Gleichungen aller Phasen in einer Matrix zusammen. Dies führt, zusammen mit der skalierbaren Parallelisierung, zu einer bisher unerreichten Zuverlässigkeit und Schnelligkeit bei komplexen Problemstellungen.
Die durch die Diskretisierung entstandenen algebraischen Gleichungen sind nichtlinear, d.h. es tauchen Produkte (oder Quotienten) von Unbekannten auf. Z.B. ist in den kompressiblen Navier-Stokes-Gleichungen die Dichte eine nichtlineare Funktion von Druck und Temperatur (u.a. beim Idealen Gasgesetz) und wird zusätzlich mit der Geschwindigkeit multipliziert, und im Konvektionsterm steht die räumliche Ableitung des Produkts zweier Geschwindigkeitskomponenten und der Dichte.
Zur späteren Lösung werden die Gleichungen linearisiert; der Massenflussterm ρU kann z.B. durch (ρU)neu=ρneuUalt+ρaltUneu-ρaltUalt linearisiert werden, so dass sowohl die Dichte ρ als auch die Geschwindigkeitskomponente U als Unbekannte (d.h. implizit) behandelt werden. Die Linearisierungen im Konvektions- und Diffusionsterm und zum Teil in den Quelltermen führen auf eine dünn besetzte Geschwindigkeits-Druck-Matrix.
Aus der Diskretisierung und Linearisierung folgen ein oder mehrere typischerweise sehr große lineare Gleichungssysteme der Form A x=b. Diese könnten direkt (z.B. durch Invertierung der Matrix A) gelöst werden. Dies ist aber nicht praktikabel (zu speicher- und rechenzeitaufwändig) und unnötig genau. Geeigneter sind sogenannte iterative Verfahren, bei denen sich eine Näherungslösung bei jeder Anwendung (Iteration) der Lösung annähert, wie das Jacobi- oder das Gauß-Seidel-Verfahren.
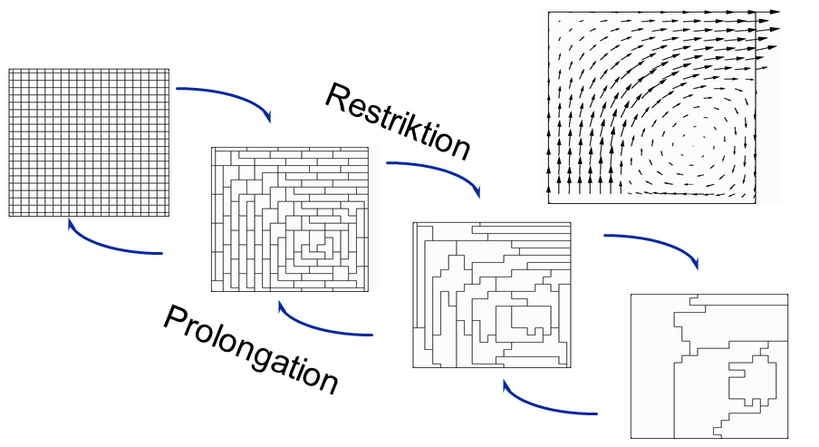
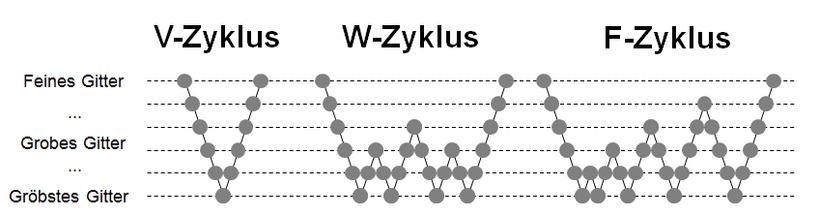
Die Erfahrung mit diesen iterativen Lösern hat gezeigt, dass Fehler mit (im Vergleich zum Gitter) kurzer Wellenlänge schnell gegen null gehen, solche mit langer Wellenlänge aber nur langsam, also viele Iterationen erfordern, häufig wird deswegen von einer Glättung gesprochen. Das Mehrgitterverfahren nutzt diesen Umstand aus, indem das Problem sukzessive auf gröbere Gitter übertragen (sogenannte Restriktion) und dort gelöst wird. Die Lösung wird dann wieder sukzessive auf die feineren Gitter interpoliert (sogenannte Prolongation), wobei jeweils nach Restriktion und Prolongation mehrere Glättungen durchgeführt werden. Da der Glättungsaufwand auf groben Gittern deutlich geringer ist und da der vorher "langwellige" Fehler auf groben Gittern schneller verschwindet, konvergiert der Löser hiermit bedeutend schneller.
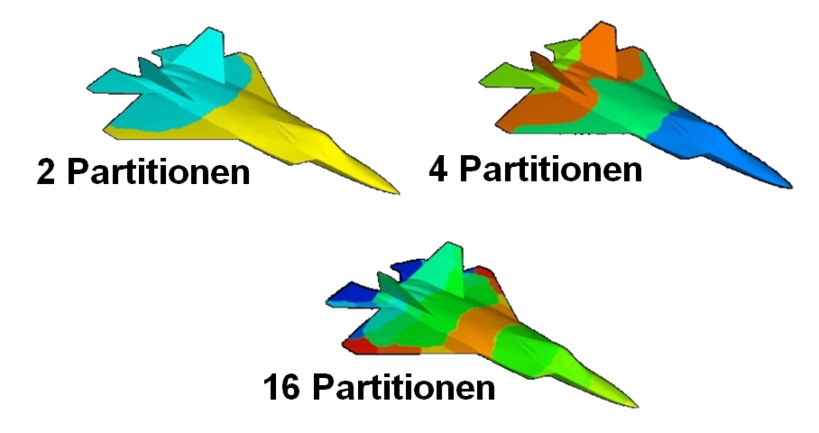
CFD-Software ist von vorn herein für den Einsatz auf Mehrprozessor-Systemen ausgelegt worden. Egal ob Sie eine homogene oder heterogene Rechnerlandschaft zur Verfügung haben, Sie können viel Zeit sparen, indem Sie mehrere Rechner (verteilte Parallelisierung) und/oder CPUs (lokale Parallelisierung) für die Berechnung zusammenschalten. Dabei wird das Berechnungsgebiet automatisch in die notwendige Anzahl von Partitionen zerlegt und wird selbständig auf die verschiedenen Rechner verteilt. Der dadurch erzielte Geschwindigkeitszuwachs ist direkt proportional zur Anzahl der verwendeten CPUs.
Ein integriertes Queueing-System ermöglicht die effiziente Remote-Nutzung von Rechenhardware durch verschiedene Benutzer. Die Berechnung werden dazu automatisch auf die ausgewählte Rechenhardware (zum Beispiel Cluster) ausgelagert und mit freien Ressourcen durchgeführt. Der Anwender erhält eine Nachricht, wenn die Berechnung abgeschlossen und die Ergebnisse transferiert wurden.
CFD-Löser bieten eine Vielzahl an numerischen und physikalischen Modellen, die zusätzlich durch Parameter angepasst werden können. Statt fester Werte oder Koeffizienten kann an den meisten Stellen auch ein komplexer Ausdruck, z.B. ein parabolisches Geschwindigkeitsprofil an einem Einlass, vorgegeben werden. Über Interpolationsfunktionen können auch tabellarische Werte direkt eingelesen und benutzt werden. Eigene Modelle können mit Hilfe von zusätzlichen algebraischen Gleichungen oder partiellen Differentialgleichungen definiert und eingebunden werden.
Sollten diese Möglichkeiten nicht ausreichen, können eigene Berechnungsroutinen über vordefinierte Programmierschnittstellen auf die Variablen des Strömungslösers zugreifen und daraus berechnete Größen an diesen zurückgeben.